CHISQ.TEST
Definition
Returns the test for independence. CHISQ.TEST returns the value from the chi-squared (χ2) distribution for the statistic and the appropriate degrees of freedom. You can use χ2 tests to determine whether hypothesized results are verified by an experiment.
Sample Usage
Syntax
CHISQ.TEST(actual_range,expected_range)
The CHISQ.TEST function syntax has the following arguments:
Actual_range Required. The range of data that contains observations to test against expected values.
Expected_range Required. The range of data that contains the ratio of the product of row totals and column totals to the grand total.
Remarks
If actual_range and expected_range have a different number of data points, CHISQ.TEST returns the #N/A error value.
The χ2 test first calculates a χ2 statistic using the formula:
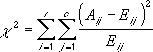
where:
Aij = actual frequency in the i-th row, j-th column
Eij = expected frequency in the i-th row, j-th column
r = number or rows
c = number of columns
A low value of χ2 is an indicator of independence. As can be seen from the formula, χ2 is always positive or 0, and is 0 only if Aij = Eij for every i,j.
CHISQ.TEST returns the probability that a value of the χ2 statistic at least as high as the value calculated by the above formula could have happened by chance under the assumption of independence. In computing this probability, CHISQ.TEST uses the χ2 distribution with an appropriate number of degrees of freedom, df. If r > 1 and c > 1, then df = (r - 1)(c - 1). If r = 1 and c > 1, then df = c - 1 or if r > 1 and c = 1, then df = r - 1. r = c= 1 is not allowed and #N/A is returned.
Use of CHISQ.TEST is most appropriate when Eij’s are not too small. Some statisticians suggest that each Eij should be greater than or equal to 5.
In order to use the CHISQ.TEST formula, start with your edited Excellentable:
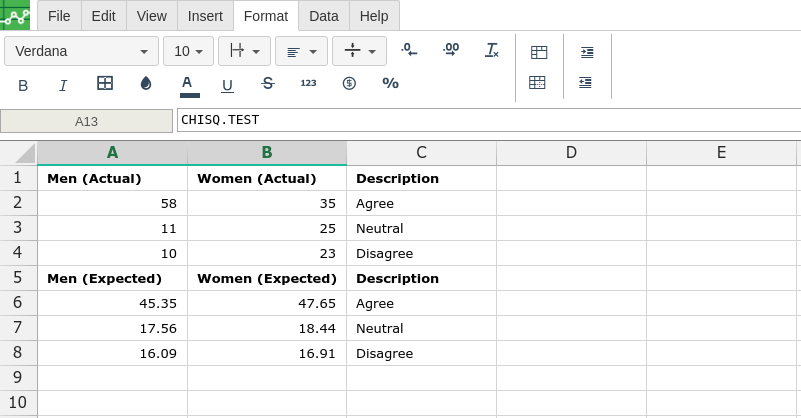
Then type in the CHISQ.TEST formula in the area you would like to display the outcome:
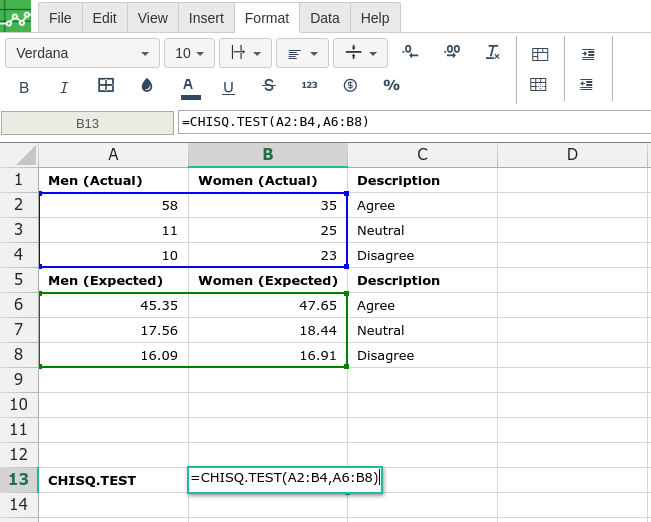
By adding the values you would like to calculate the CHISQ.TEST formula for, Excellentable will generate the outcome:
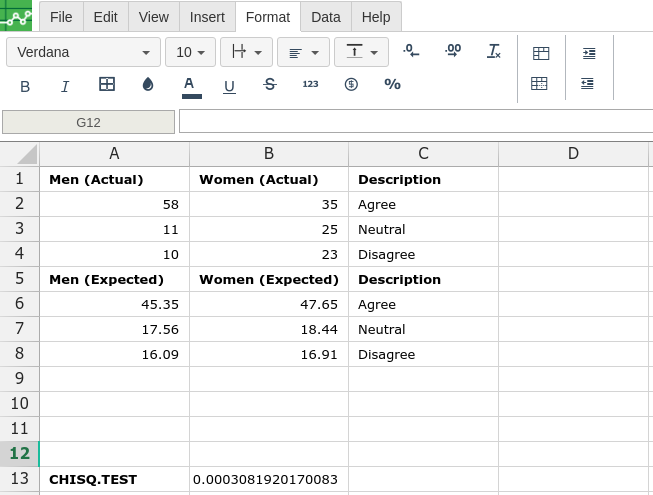
A
|
B
|
C
|
|
|---|---|---|---|
1
|
|||
2
|
|||
3
|
|||
4
|
|||
5
|
|||
6
|
|||
7
|
|||
8
|
|||
9
|
|||
10
|
|||
11
|
|||
12
|
|||
13
|
