F.INV.RT
Definition
Returns the inverse of the (right-tailed) F probability distribution. If p = F.DIST.RT(x,...), then F.INV.RT(p,...) = x. The F distribution can be used in an F-test that compares the degree of variability in two data sets. For example, you can analyze income distributions in the United States and Canada to determine whether the two countries have a similar degree of income diversity.
Sample Usage
Syntax
F.INV.RT(probability,deg_freedom1,deg_freedom2)
The F.INV.RT function syntax has the following arguments:
Probability Required. A probability associated with the F cumulative distribution.
Deg_freedom1 Required. The numerator degrees of freedom.
Deg_freedom2 Required. The denominator degrees of freedom.
Remarks
If any argument is non-numeric, F.INV.RT returns the #VALUE! error value.
If Probability is < 0 or probability is > 1, F.INV.RT returns the #NUM! error value.
If Deg_freedom1 or Deg_freedom2 is not an integer, it is truncated.
If Deg_freedom1 is < 1, or Deg_freedom2 is < 1, F.INV.RT returns the #NUM! error value.
If Deg_freedom2 is < 1 or Deg_freedom2 is ≥ 10^10, F.INV.RT returns the #NUM! error value.
F.INV.RT can be used to return critical values from the F distribution. For example, the output of an ANOVA calculation often includes data for the F statistic, F probability, and F critical value at the 0.05 significance level. To return the critical value of F, use the significance level as the probability argument to F.INV.RT.
Given a value for probability, F.INV.RT seeks that value x such that F.DIST.RT(x, deg_freedom1, deg_freedom2) = probability. Thus, precision of F.INV.RT depends on precision of F.DIST.RT. F.INV.RT uses an iterative search technique. If the search has not converged after 64 iterations, the function returns the #N/A error value.
In order to use the F.INV.RT formula, start with your edited Excellentable:
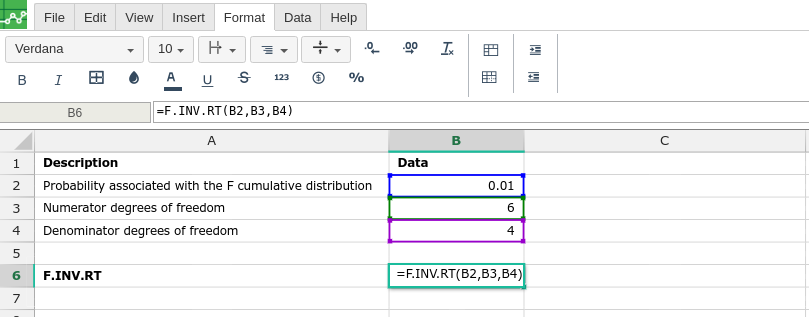
Then type in the F.INV.RT formula in the area you would like to display the outcome:
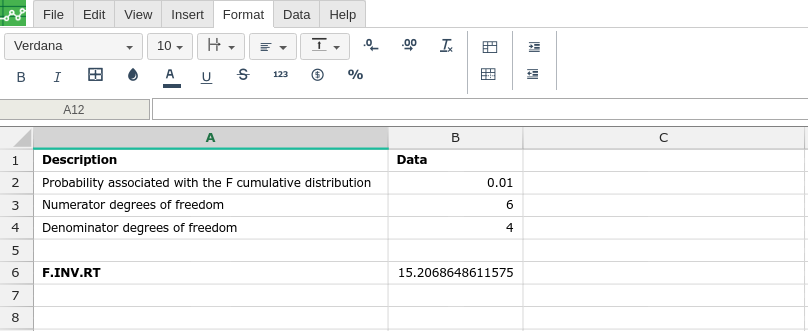
By adding the values you would like to calculate the F.INV.RT formula for, Excellentable will generate the outcome:
A
|
B
|
|
|---|---|---|
1
|
||
2
|
||
3
|
||
4
|
||
5
|
||
6
|
