LINEST

Given partial data about a linear trend, calculates various parameters about the ideal linear trend using the least-squares method.

Sample Usage

Syntax

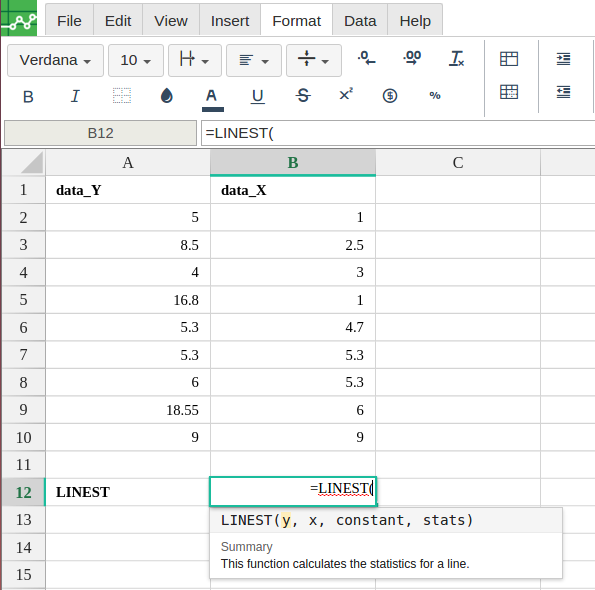
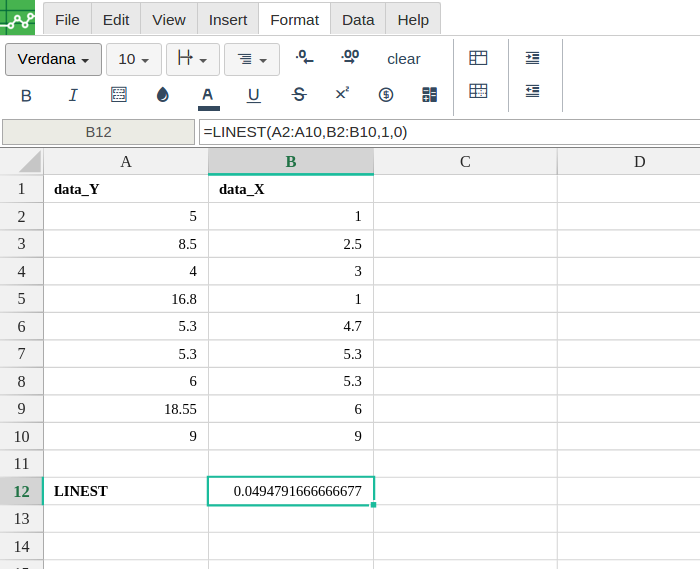
LINEST(known_data_y, [known_data_x], [calculate_b], [verbose])

• known_data_y - The array or range containing dependent (y) values that are already known, used to curve fit an ideal linear trend.

  • If known_data_y is a two-dimensional array or range, known_data_x must have the same dimensions or be omitted.

  • If known_data_y is a one-dimensional array or range, known_data_x may represent multiple independent variables in a two-dimensional array or range. I.e. if known_data_y is a single row, each row in known_data_x is interpreted as a separated independent value, and analogously if known_data_y is a single column.

• known_data_x - [ OPTIONAL - {1,2,3,...} with same length as known_data_y by default ] - The values of the independent variable(s) corresponding with known_data_y.

  • If known_data_y is a one-dimensional array or range, known_data_x may represent multiple independent variables in a two-dimensional array or range. I.e. if known_data_y is a single row, each row in known_data_x is interpreted as a separated independent value, and analogously if known_data_y is a single column.

• calculate_b - [ OPTIONAL - TRUE by default ] - Given a linear form of y = m*x+b, calculates the y-intercept (b) ifTRUE. Otherwise, forces b to be 0 and only calculates the m values if FALSE, i.e. forces the curve fit to pass through the origin.

• verbose - [ OPTIONAL - FALSE by default ] - A flag specifying whether to return additional regression statistics or only the linear coefficients and the y-intercept (default).

  • If verbose is TRUE, in addition to the set of linear coefficients for each independent variable and the y-intercept,LINEST returns

    • The standard error for each coefficient and the intercept,

    • The coefficient of determination (between 0 and 1, where 1 indicates perfect correlation),

    • Standard error for the dependent variable values,

    • The F statistic, or F-observed value indicating whether the observed relationship between dependent and independent variables is random rather than linear,

    • The degrees of freedom, useful in looking up F statistic values in a reference table to estimate a confidence level,

    • The regression sum of squares, and

    • The residual sum of squares.

See Also

TREND: Given partial data about a linear trend, fits an ideal linear trend using the least squares method and/or predicts further values.

LOGEST: Given partial data about an exponential growth curve, calculates various parameters about the best fit ideal exponential growth curve.

GROWTH: Given partial data about an exponential growth trend, fits an ideal exponential growth trend and/or predicts further values.

In order to use the LINEST formula, start with your edited Excellentable:

	A	B
1	data_Y	data_X
2	5	1
3	8.5	2.5
4	4	3
5	16.8	1
6	5.3	4.7
7	5.3	5.3
8	6	5.3
9	18.55	6
10	9	9
11
12	LINEST	0.049479167