TREND
Definition
Given partial data about a linear trend, fits an ideal linear trend using the least squares method and/or predicts further values.
Sample Usage
Syntax
TREND(known_data_y, [known_data_x], [new_data_x], [b])
known_data_y- The array or range containing dependent (y) values that are already known, used to curve fit an ideal linear trend.If
known_data_yis a two-dimensional array or range,known_data_xmust have the same dimensions or be omitted.If
known_data_yis a one-dimensional array or range,known_data_xmay represent multiple independent variables in a two-dimensional array or range. I.e. ifknown_data_yis a single row, each row inknown_data_xis interpreted as a separated independent value, and analogously ifknown_data_yis a single column.
known_data_x- [ OPTIONAL -{1,2,3,...}with same length asknown_data_yby default ] - The values of the independent variable(s) corresponding withknown_data_y.- If
known_data_yis a one-dimensional array or range,known_data_xmay represent multiple independent variables in a two-dimensional array or range. I.e. ifknown_data_yis a single row, each row inknown_data_xis interpreted as a separated independent value, and analogously ifknown_data_yis a single column.
- If
new_data_x- [ OPTIONAL - same asknown_data_xby default ] - The data points to return theyvalues for on the ideal curve fit.- The default behavior is to return the ideal curve fit values for the same
xinputs as the existing data for comparison of knownyvalues and their corresponding curve fit estimates.
- The default behavior is to return the ideal curve fit values for the same
b- [ OPTIONAL -TRUEby default ] - Given a general exponential form ofy = m*x+bfor a curve fit, calculatesbifTRUEor forcesbto be0and only calculates themvalues ifFALSE, i.e. forces the curve fit to pass through the origin.
See Also
LOGEST: Given partial data about an exponential growth curve, calculates various parameters about the best fit ideal exponential growth curve.
LINEST: Given partial data about a linear trend, calculates various parameters about the ideal linear trend using the least-squares method.
GROWTH: Given partial data about an exponential growth trend, fits an ideal exponential growth trend and/or predicts further values.
In order to use the TREND formula, start with your edited Excellentable:
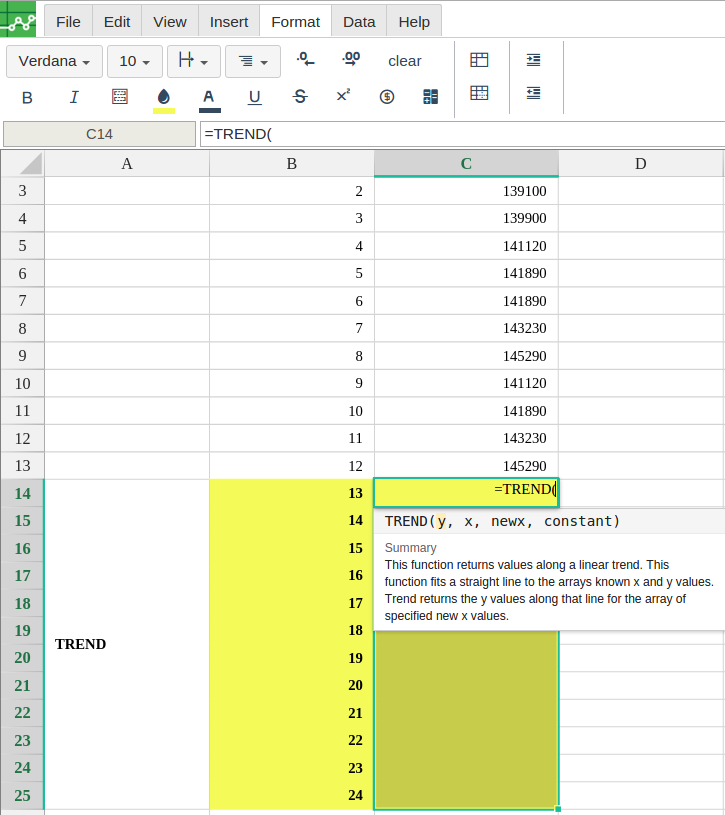
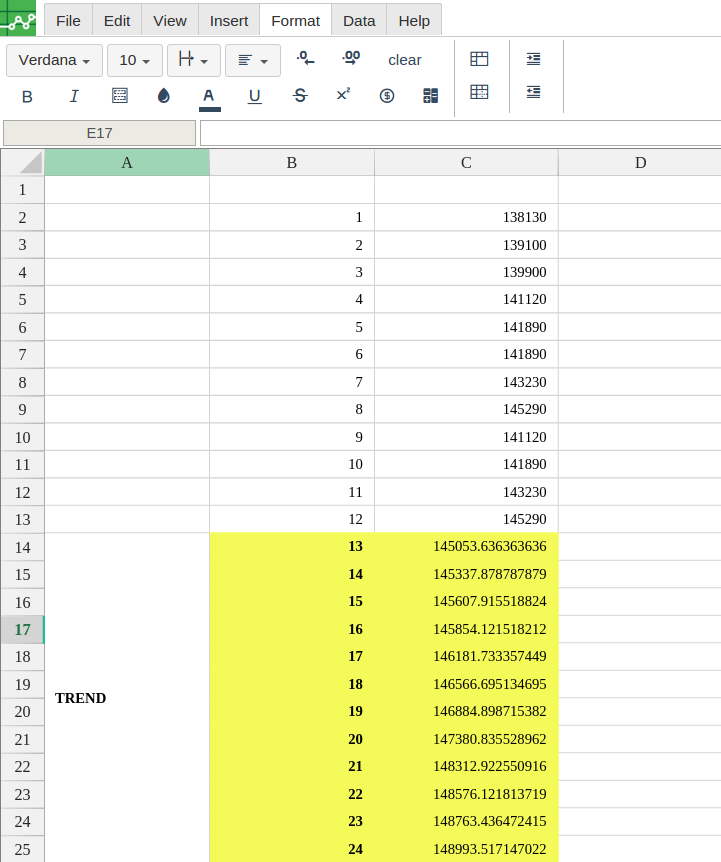
A
|
B
|
C
|
|
|---|---|---|---|
1
|
|||
2
|
|||
3
|
|||
4
|
|||
5
|
|||
6
|
|||
7
|
|||
8
|
|||
9
|
|||
10
|
|||
11
|
|||
12
|
|||
13
|
|||
14
|
|||
15
|
|||
16
|
|||
17
|
|||
18
|
|||
19
|
|||
20
|
|||
21
|
|||
22
|
|||
23
|
|||
24
|
|||
25
|
