LOGNORMDIST

Definition of LOGNORMDIST

Returns the value of the log-normal cumulative distribution with given mean and standard deviation at a specified value.

Sample Usage

LOGNORMDIST(4,4,6)

LOGNORMDIST(A2,A3,A4)

Syntax

LOGNORMDIST(x, mean, standard_deviation)

• x - The input to the log-normal cumulative distribution function.

• mean - The mean (mu) of the log-normal cumulative distribution function.

• standard_deviation - The standard deviation (sigma) of the log-normal cumulative distribution function.

Notes

• A log-normal distribution function is a probability distribution function of a random variable whose logarithm is normally distributed.

See Also

WEIBULL: Returns the value of the Weibull distribution function (or Weibull cumulative distribution function) for a specified shape and scale.

POISSON: Returns the value of the Poisson distribution function (or Poisson cumulative distribution function) for a specified value and mean.

NORMSDIST: Returns the value of the standard normal cumulative distribution function for a specified value.

NORMINV: Returns the value of the inverse normal distribution function for a specified value, mean, and standard deviation.

NORMDIST: Returns the value of the normal distribution function (or normal cumulative distribution function) for a specified value, mean, and standard deviation.

NEGBINOMDIST: Calculates the probability of drawing a certain number of failures before a certain number of successes given a probability of success in independent trials.

LOGINV : Returns the value of the inverse log-normal cumulative distribution with given mean and standard deviation at a specified value.

BINOMDIST: Calculates the probability of drawing a certain number of successes (or a maximum number of successes) in a certain number of tries given a population of a certain size containing a certain number of successes, with replacement of draws.

To use the LOGNORMDIST Formula, simply begin with your edited Excellentable:  

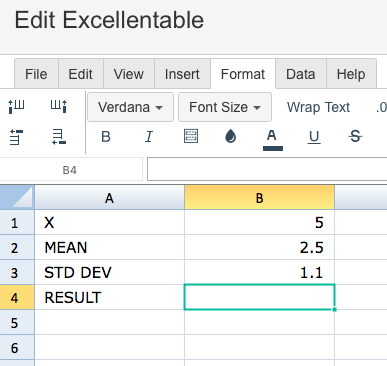
Then begin typing the LOGNORMDIST formula in the area you would like to display the outcome: 

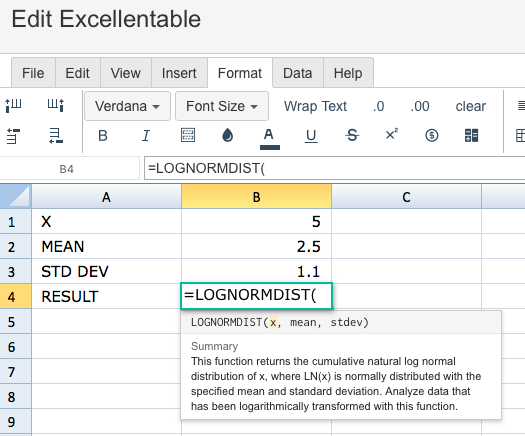
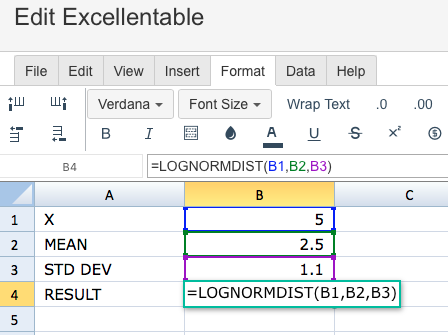
	A	B
1	X	5
2	MEAN	2.5
3	STD DEV	1.1
4	RESULT	0.209084509